The design of norm preserving omnidirectional catadioptric vision has become an hot topic in robotics, namely in the RoboCup community. The purpose of this page is to disseminate a program capable of designing such mirrors.
The problem geometry consists on a video camera point upwards, aligned with a omnidirectional mirror. The mirror shape is designed to map points at the floor plane to points in the camera image plane such that the norm is preserved. On other words, the image perceived by the camera corresponds to an orthographic projection of the floor.
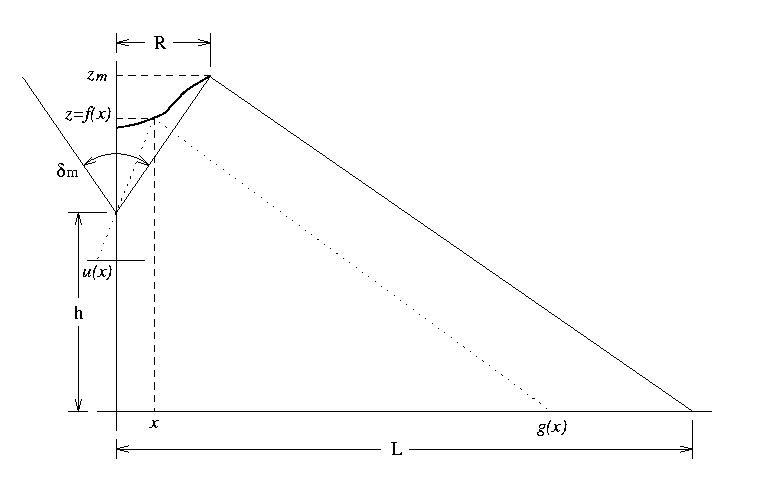
To solve this problem, a differential equation is derived. For a given point at the mirror surface (x,f(x)) -- where f(x) corresponds to the mirror profile -- this differential equation expresses the relationship between an image point u(x) and a point at the floor plane g(x). Since a linear relationship k u(x)=g(x) is sought, for a given proportional constant k, and since u(x) and u(x) depend on the mirror profile f(x) and its derivative f'(x), a differential equation on f(x) can be derived.
Given this differential equation along with a boundary condition obtained from the desired specifications, a numeric solution can be obtained. The purpose of this program is to automate this process. The output is a set of points describing the mirror profile, in order to be used by a CNC machine, for instance.
The mirror specifications are expressed in the following parameters:
The program is available as a Mathematica notebook. In order to run the program a full version of Mathematica is required. However, a freely available version of Mathematica notebooks can be found here.
NOTE: In some browsers, a "shift-click" is required to correctly download the notebook.